Principal Components Analysis
We use here an example of decathlon data which refers to
athletes' performance during two athletic meetings.
You can load the data set as a text file here.
Presentation of the data
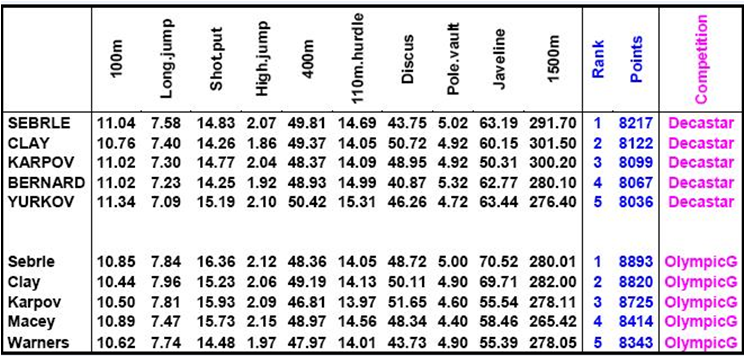
The data set is made of 41 rows and 13 columns.
The columns 1 to 12 are continuous variables: the first ten columns
correspond to the performance of the athletes for the 10 events of the
decathlon and the columns 11 and 12 correspond respectively to the rank
and the points obtained. The last column is a categorical variable
corresponding to the athletic meeting (2004 Olympic Game or 2004
Decastar).
To load the package FactoMineR
and the data set, write the following line code: library(FactoMineR)
data(decathlon)
Objectives
PCA allows to describe a dataset, to summarize a dataset, to
reduce the dimensionality.
We want to perform a PCA on all the individuals of the data
set to answer several questions:
- Individuals' study (athletes' study): two athletes will be close to each other if their results to the events are close. We want to see the variability between the individuals. Are there similarities between individuals for all the variables? Can we establish different profiles of individuals? Can we oppose a group of individuals to another one?
- Variables' study (performances' study): We want to see if there are linear relationships between variables. The two objectives are to summarize the correlation matrix and to look for synthetic variables: can we resume the performance of an athlete by a small number of variables?
- Link between this two studies: can we characterize groups of individuals by variables?
PCA
We are going to study athlete's profiles according to their
performances only. The active variables will thus be only those which
concern the ten events of the decathlon.
The other variables ("Rank", "Points"
and "Competition") do not belong to this
athletes' profiles and use an information already given by the other
variables (in the case of "Rank" and "Points")
but it is interesting to confront them to the principal components. We
will use them as supplementary variables.
Here the variables are not measured in the same units. We have to scale them in order to give the same influence to each one.
Active individuals and variables
We type the following line code to perform a PCA on all the
individuals, using only the active variables, i.e.
the first ten: res.pca =
PCA(decathlon[,1:10], scale.unit=TRUE, ncp=5, graph=T)
#decathlon: the data set
used
#scale.unit: to choose whether to scale the data or not
#ncp: number of dimensions kept in the result
#graph: to choose whether to plot the graphs or not
The first two dimensions resume 50% of the total inertia (the inertia is the total variance of dataset i.e. the trace of the correlation matrix).
The variable "X100m" is correlated negatively to the variable "long.jump". When an ahtlete performs a short time when running 100m, he can jump a big distance. Here one has to be careful because a low value for the variables "X100m", "X400m", "X110m.hurdle" and "X1500m" means a high score: the shorter an athlete runs, the more points he scores.
The first axis opposes athletes who are "good everywhere" like Karpov during the Olympic Games between those who are "bad everywhere" like Bourguignon during the Decastar. This dimension is particularly linked to the variables of speed and long jump which constitute a homogeneous group.
The second axis opposes athletes who are strong (variables "Discus"
and "Shot.put") between those who are not.
The variables "Discus", "Shot.put"
and "High.jump" are not much correlated to the
variables "X100m", "X400m",
"X110m.hurdle" and "Long.jump".
This means that strength is not much correlated to speed.
At the end of this first approach, we can divide the factorial plan into four parts: fast and strong athletes (like Sebrle), slow athletes (like Casarsa), fast but weak athletes (like Warners) and slow and weak (relatively speaking!) athletes (like Lorenzo).
supplementary variables
Supplementary variables have no influence on the principal components of the analysis. They are going to help to interpret the dimensions of variability.
We can add two different kinds of variables: continuous ones and categorical ones.
As supplementary continuous variables, we would like to add
the variables "Rank" and "Points".
We type the following line code: res.pca
= PCA(decathlon[,1:12], scale.unit=TRUE, ncp=5, quanti.sup=c(11: 12), graph=T)
#decathlon:
the data set used
#scale.unit: to choose whether to scale the datas or not
#ncp: number of dimensions kept in the result
#quanti.sup: vector of the indexes of the quantitative supplementary
variables
#graph: to choose whether to plot the graphs or not
The winners of the decathlon are those who scored the most (or
those whose rank is low).
The variables the most linked to the number of points are the variables
which refer to the speed ("X100m", "X110m.hurdle",
"X400m") and the long jump. On the contrary, "Pole-vault"
and "X1500m" do not have a big influence on the
number of points. Athletes who are strong for these two events are not
favoured.
As a supplementary categorical variable, we add the variable
"Competition": res.pca =
PCA(decathlon, scale.unit=TRUE, ncp=5, quanti.sup=c(11: 12),
quali.sup=13, graph=T) #decathlon: the data set used
#scale.unit: to choose whether to scale the datas or not
#ncp: number of dimensions kept in the result
#quanti.sup: vector of the indexes of the quantitative supplementary
variables
#quali.sup: vector of the indexes of the qualitative supplementary
variables
#graph: to choose whether to plot the graphs or not
The categories' centres of gravity of this new
variable appear
on the graph of the individuals. They are located at the barycentre of
the individuals who took them and they represent an average
individual.
We can also colour the individuals according to the categories' centres
of gravity: plot.PCA(res.pca,
axes=c(1, 2), choix="ind", habillage=13) #res.pca: the result of a PCA
#axes: the axes to plot
#choix: the graph to plot ("ind" for the individuals, "var" for the
variables)
#habillage: to choose the colours of the individuals: no colour
("none"), a colour for each individual ("ind") or to colour the
individuals according to a categorical variable (give the number of the
qualitative variable)
When looking at the points representing "Decastar"
and "Olympic Games", we notice that this last one
has higher coordinates on the first axis than the first one. This shows
an evolution in the performances of the athletes. All the athletes who
participated to the two competitions have then slightly better
results for
the Olympic Games.
However, there is no difference between the points "Decastar"
and "Olympic Games" for the second axis. This
means that the athletes have improved their performance but did not
change profile (except for Zsivoczky who went from slow and strong
during the Decastar to fast and weak during the Olympic Games).
We can see that the points which represent the same individual are in the same direction. For example, Sebrle got good results in both competition but the point which represents his performance during the O.G. is more extreme. Sebrle got more points during the O.G. than during the Decastar.
Two interpretations can be made:
- Athletes who participate in the O.G. are better than those who participate in the Decastar
- Athletes do their best for the O.G. (more motivated, more trained)
The dimdesc() function allows to
describe the dimensions.
We can describe the dimensions given by the variables by writing: dimdesc(res.pca, axes=c(1,2))
#res.pca: the result of a
PCA
#axes: the axes chosen
The dimdesc() function calculates the
correlation coefficient between a variable an a dimension and performs
a significance test.
These tables give the correlation
coefficient and the p-value
of the variables which are significantly correlated to the principal
dimensions. Both active and supplementary variables whose p-value is
smaller than 0.05 appear.
The tables of the description of the two principal axes show that the variables "Points" and "Long.jump" are the most correlated to the first dimension and "Discus" is the most correlated to the second one. This confirms our first interpretation.
This function is very useful in settings where there are many variables and allows to make the interpretation easier.
If we do not want an individual (or several ones) to
participate in the analysis, it is possible to add it as a
supplementary individual. It will not be active in the analysis but
will bring supplementary information.
To add supplementary individuals, use the following argument of the PCA
function: ind.sup
All the detailed results can be found in res.pca.
We can get
the eigenvalues, the results of the active
and supplementary individuals, the results of the active variables and
the results of the
categorical and continuous supplementary variables by typing: res.pca
names(res.pca)
res.pca$eig, res.pca$ind,
res.pca$ind.sup, res.pca$var, res.pca$quali.sup, res.pca$quanti.sup
To go further
In most PCAs, the weight of the individuals is equal to
1/(number of individuals). However, it is sometimes necessary to give a
specific weight to some individuals.
To do so, the user will have to use the argument: row.w
It can also be interesting to give a specific weight to some
variables.
Here, the user will have to use the argument: col.w
To see whether the categories of the supplementary variable
are significantly different from each other, we can draw confidence
ellipses around them.
To do so, type: plotellipses(res.pca)