Multiple Factor Analysis
Multiple Factor Analysis is dedicated to datasets where variables are structured into groups. Several sets of variables (continuous or categorical) are therefore simultaneously studied.
This specific method is useful in many fields where variables are structured into groups, for example:
- Genomic: protein variables, DNA variables
- Sensory analysis: sensorial and physico-chemical variables
- Questionnaires: student health (addicted consumptions variables, psychological conditions variables, sleep, identification variables...)
- Comparison of coding (continous variables, categorical variables)
Taking into account the structure of the data allows to:
- Balance the influence of each group of variables
- Study the links between the sets of variables
- Give the classical graphs but also specific ones:
- Partial representation (individuals seen by one group of variables)
- Groups of variables
For further information on the MFA, see the book:
Pagès J. (2015) Multiple Factor Analysis by Example Using R.. Chapman & Hall/CRC. (see more details here)
or the following tutorials:
SFDS 2008 slides about FactoMineR
User! 2007 slides about FactoMineR
The example illustrated here deals with sensory evaluation of
red wines.
Load the data set as a text file by clicking here.
Presentation of the data
The data set is made of 21 rows (wines) and 31 columns.
The first two columns are categorical variables : label (Saumur,
Bourgueil or Chinon) and soil (Reference, Env1, Env2 or Env4).
The 29 next columns are continuous sensory variables. For each wine,
the value is the mean for all the judges.
To load the package and the data set, type the following line code: library(FactoMineR)
data(wine)
Objectives
We want to characterize the wines. We are looking for a typology of the wines.
The appropriate principal component method to characterize the wines
by continuous variables is the Principal Components Analysis.
However, we can see that the data set is structured. Variables form
different groups:
- One categorical group (variables label and soil)
- One group concerning the odor before shaking (variables Odor.Intensity.before.shaking, Aroma.quality.before.shaking, Fruity.before.shaking, Flower.before.shaking and Spice.before.shaking)
- One group concerning visual evaluation (variables Visual.intensity, Nuance and Surface.feeling)
- One group concerning the odor after shaking (variables Odor.Intensity, Quality.of.odour, Fruity, Flower, Spice, Plante, Phenolic, Aroma.intensity, Aroma.persistency and Aroma.quality)
- One group concerning the taste (variables Attack.intensity, Acidity, Astringency, Alcohol, Balance, Smooth, Bitterness, Intensity and Harmony)
- And one last group concerning an overall judgement (variables Overall.quality and Typical)
New objectives arise like comparing groups of variables (two sets of variables are close to each other if two wines which are close to each other according to the first set of variables are close to each other according to the second one) and highlight a typology of the groups or comparing simultaneously the typologies of wines seen by each group of variables taken one by one.
MFA
We are going to study the wines' profiles according to sensory evaluation. We will use as active groups the odor, visual, odor after shaking and taste groups and origin and overall groups as supplementary ones.
Type:
res = MFA(wine,
group=c(2,5,3,10,9,2), type=c("n",rep("s",5)), ncp=5,
name.group=c("origin","odor","visual","odor.after.shaking",
"taste","overall"), num.group.sup=c(1,6))
#wine: the data
set used
#group: a vector indicating the number of variables in each group
#type: the type of the variables in each group. "s" for scaled
continuous variables, "c" for centered (unscaled) continuous variables
and "n" for categorical variables
#ncp: number of dimensions kept in the result
#name.group: names of the groups
#num.group.sup: indexes of the supplementary groups
These first results can be interpreted the same way as the ones of a PCA.
The representation of variables shows that most of the
variables are highly correlated to the first dimension, whatever group
the belong to. This dimension represents "intensity" and "harmony",
positive notions which are commonly used when speaking of wines.
The variables the most correlated to the second dimension are Spice
before shaking and Odor intensity before shaking
for the odor group, Spice,
Plant and Odor intensity for
the odor after shaking group and Bitterness
for the taste group. This dimension
represents a spicy, vegetal characteristic essentially due to olfaction.
The coordinates of individuals and categories can be linked to
this interpretation of the two first principal components through the
second graph.
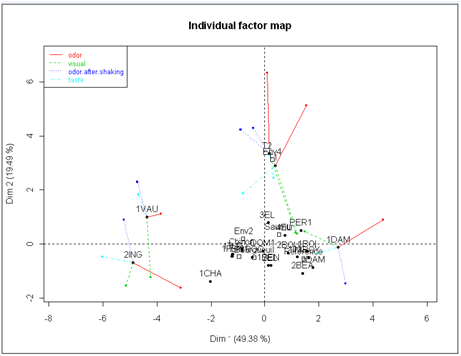
The wine 1DAM was evaluated as the most "intense" and "harmonious"
contrary to wines 1VAU and 2ING which are the least "intense" and
"harmonious". The second axis is essentially due to wines T1 and T2. As
these two wines were in fact the same one evaluated twice by the
assessors, the second dimension will be designed as the "particular
case of the wine T".
Most of the categories are close to the origin of the principal component map,
which means that these categories are not related to "intensity",
"harmony" or the "wine T". The category Env4 has
high coordinates on the second axis but only related to T1 and T2. The
category Reference, a priori
related to an excellent wine-producing soil, has high coordinates on
the first axis and thus positively correlated to "intensity" and
"harmony", which confirms the a priori.
The graph of partial individuals represents each wine viewed by each
group and its barycenter. By default, the two wines with the smallest within inertia and the two wines with the largest within inertia are represented. If you want to plot all the partial points, use the folowwing line of code:
plot(res,choix="ind",partial="all")
1DAM was evaluated as particularly "intense" and "harmonious" especially by the odor group: its coordinates on the first axis are more extreme from this group's point of view than from the other groups' one. From the odor group's point of view, 2ING was more "intense" and "harmonious" than 1VAU but from the taste group's point of view, 1VAU was more "intense" and "harmonious" than 2ING.
All the groups have quite the same vision of the categories except for Env4 which resumes what we already said from the individuals principal component map.
This graph shows the quality of representation of each group.
The four active groups have close coordinates on the first dimension
which means that their contribution to the first principal component is
quite the same. It also means that the first principal component of the MFA is common to all the groups.
As for the second dimension, it is the olfactory groups that have the
highest coordinates. These two groups contribute the most to the second
principal component.
This graph is diplayed to look at the link between the principal
components of the MFA and the ones of each single group.
Except for the origin group, the first
dimension of each group is highly correlated to the MFA's first one.
The second dimension of the MFA is essentially correlated to the second
dimension of the olfactory groups.