Dimension Description
The dimdesc function helps to interpret the dimensions of a PCA, a MCA, a CA, a MFA or a HMFA.
It describes dimensions by both categorical and/or continuous variables.
Objectives
This function is very useful when there is a lot of variables.
It allows to see which variables the axes are the most linked to: which continuous variables are the most correlated to each axis and which categorical variables and categories describe the best each axis.
We are going to perform dimdesc function on the axes of an MCA performed on the data set "tea".
dimdesc
First load the package and the data set by typing:
library(FactoMineR)
data(tea)
Then perform the MCA:
res.mca = MCA(tea, quanti.sup=19, quali.sup=c(20:36))
And launch the dimdesc() function:
res = dimdesc(res.mca, axes=1:2, proba=0.05)
#res.mca: the result of a previous analysis of which axes we want to characterize
#axes: a vector with the dimensions to describe
#proba: the significance threshold considered to characterize the dimensions (by default 0.05)
Description by continuous variables
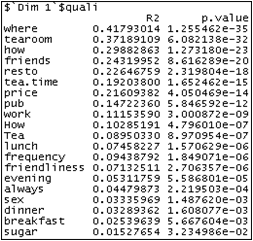
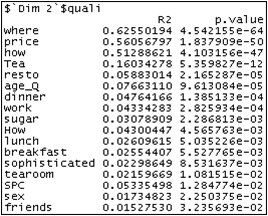
The correlation coefficient between each continuous variable and the dimension of the MCA is calculated for each dimension. Then, the correlation coefficients significantly different from zero are sorted and returned.
The only continuous variable of the data set is the age variable.
It is not significantly correlated to the first component but it is significantly correlated to the second one.
Description by categorical variables and categories
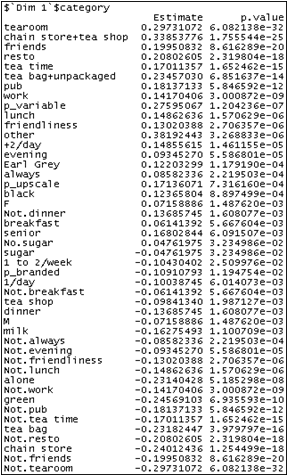
For the categorical variables, an anova model with one factor is done for each dimension; the coordinates of the individuals are explained by the categorical variable.
A F-test is derived to see whether the variable has an influence on the dimension and T-tests are done category by category (with the contrast sum alpha_i=0). We can see if the coordinates of the individuals of the sub-population defined by one category are significantly different from the overall (i.e. different from 0). The variables and the categories are sorted by p-value and only the significant ones are kept.
The first component is characterized by "where" then " tea room" then "how" etc... Some supplementary variables, like sex are also linked to this axis. "tea room" has a positive coordinate on this axis whereas "not tea room" has a negative one. This gives the direction of the axis: individuals with high coordinates on the first component will tend to go to tea rooms.
The second component is characterized by where then price then how etc... Individuals with high coordinates on this axis will tend to buy unpackaged tea in tea shops.